Filtri sa beskonačnim impulsnim odzivom (IIR) filtri

Digitalna obrada signala, Vladimir Petrović

U ovom notebook-u ćemo se baviti sintezom sistema sa beskonačnim impulsnim odzivom.

Uvod

Ranije smo definisali linearne vremenski nepromenljive sisteme i videli da se oni mogu okarakterisati svojim impulsnim odzivom i funkcijom prenosa. Funkcija prenosa se lako može dovesti u vezu sa frekvencijskom karakteristikom sistema korišćenjem veze između Z i Furijeove transformacije. Videli smo kako možemo uticati na frekvencijsku karakteristiku postavljanjem nula i polova u karakteristične tačke u Z ravni. Na taj način smo napravili primitivne filtre: propusnik niskih učestanosti (NF), propusnik visokih učestanosti (VF), propusnik opsega učestanosti (PO) i nepropusnik opsega učestanosti (NO). Međutim, ovaj metod projektovanja filtara nije sistematičan, pa se filtri sa beskonačnim impulsnim odzivom projektuju na drugačiji način.

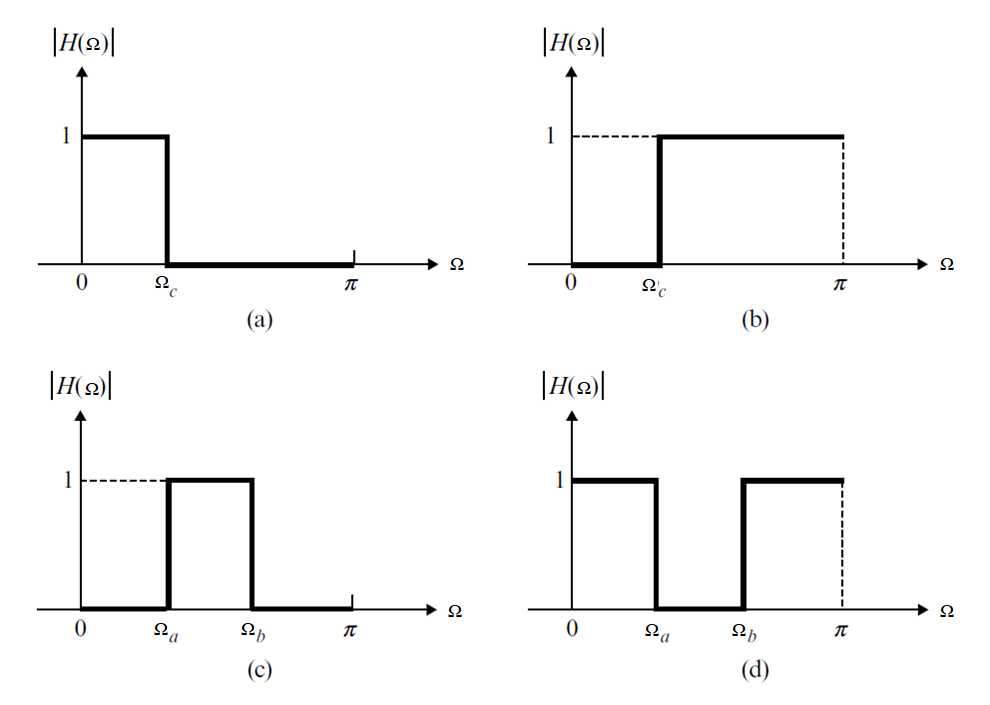
na slici ispod su prikazani idealni NF (a), VF (b), NO (c) i PO (d) filtri. U propusnim opsezima im je frekvencijska karakteristika jednaka 1 dok je u nepropusnim opsezima jednaka 0. Prelaz između nepropusnih i propusnih opsega je diskontinuitet i dešava se na učestanostima koje nazivamo graničnim učestanostima. Jasno je da se u realnosti ne može napraviti ovakva funkcija prenosa. Zbog toga se svi filtri projektuju tako da postoje male varijacije amplitudske karakteristike i u propusnim i u nepropusnim opsezima, a prelaz između propusnog i nepropusnog opsega nije diskontinuitet već neka kontinualna kriva.

Realnija frekvencijska karakteristika jednog NF filtra je prikazana na slici ispod (a) i (b). U svakoj funkciji prenosa razlikujemo propusni opseg u kome se signal pojačava, ostaje isti ili se neznatno slabi, nepropusni opseg u kome se signal značajno slabi (potiskuje) i prelaznu zonu. Funkciju prenosa specificiramo, tj. zadajemo zahteve za varijacije amplitudske karakteristike, samo u propusnom i nepropusnom opsegu. U prelaznoj zoni se vi zahtevi ne zadaju, ali se obično zahteva da u opsezima učestanosti koji pripadaju prelaznim zonama funkcija prenosa bude monotona. Specifikacije (gabariti) filtra se zadaju na osnovu potreba sistema koji se projektuje i one su sledeće:

Na slikama (a) i (b) su prikazani različiti načini zadavanja specifikacija filtra gde je prvi način najčešće karakterističan za filtre sa konačnim impulsnim odzivom, a drugi za filtre sa beskonačnim impulsnim odzivom.

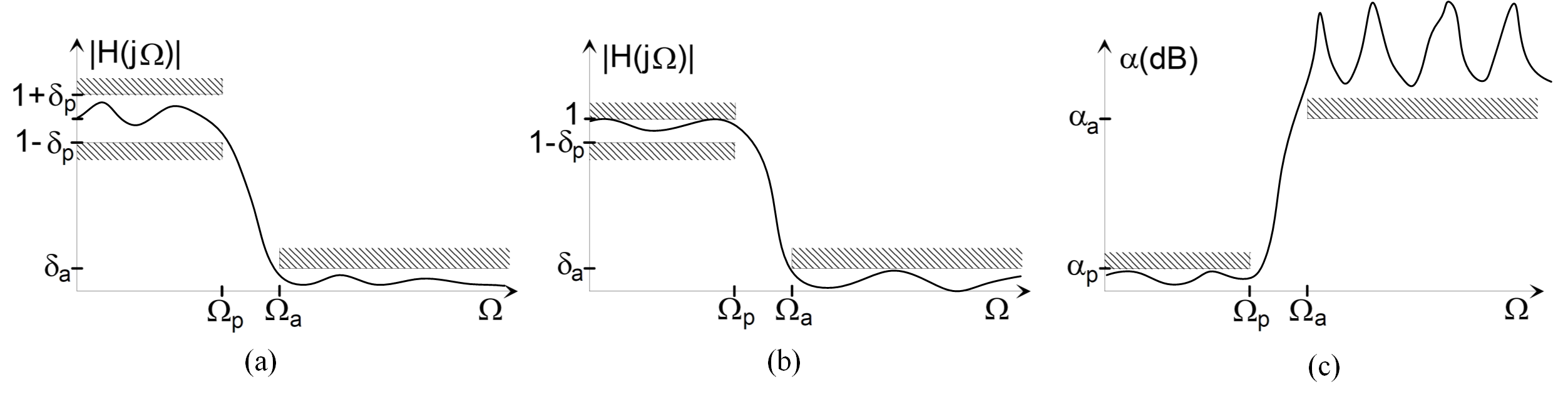
Najčešći način zadavanja specifikacija je ipak u logaritamskom domenu (slika (c)) i to kroz veličine koje nazivamo slabljenjem. Slabljenje izraženo u decibelima se dobija iz recipročne vrednosti amplitudske karakteristike:

$$ \alpha = 20\log\left(\frac{1}{|H(j\Omega)|}\right). $$

Tako se umesto varijacija amplitude specificiraju sledeći parametri:

Veza sa varijacama amplitude je data sledećim izrazima:

$$ \alpha_a = -20\log\left( \delta_a \right) $$$$ \alpha_p = 20\log\left( \frac{1 + \delta_p}{1 - \delta_p} \right), $$

za prenosnu funkciju (a) ili

$$ \alpha_p = 20\log\left( \frac{1}{1 - \delta_p} \right) $$

za prenosnu funkciju (b).

Obrnuto, iz slabljenja se lako mogu dobiti vrednosti varijacija amplituda:

$$ \delta_a = 10^{-0,05\alpha_a}, \; \; \delta_p = \frac{10^{0,05\alpha_p} - 1}{10^{0,05\alpha_p} + 1}, \; \; \delta_p = 1 - 10^{-0,05\alpha_p}. $$

Kada su zadate specifikacije filtra postupak projektovanja se svodi na pronalaženje funkcije prenosa koja će zadovoljiti zadate specifikacije. Potrebno je napomenuti da se pored graničnih učestanosti propusnog i nepropusnog opsega, često koristi i parametar centralna graniča učestanost koji je ništa drugo do aritmetička sredina navedene dve granične učestanosti:

$$ \Omega_c = \frac{\Omega_a + \Omega_p}{2}. $$

IIR filtri se najčešće projektuju tako što se najpre isprojektuju analogne funkcije prenosa, a zatim se one diskretizuju nekom transformacijom. Analogne funkcije prenosa se najčešće projektuju polazeći od neke prototipske funkcije NF tipa kod koje granična učestanost propusnog opsega postavljena na $\omega_p = 1\, \mathrm{rad/s}$ (tzv. normalizovanog NF prototipa). Iz prototipske funkcije se postupkom koji nazivamo transformacijom učestanosti dobija frekvencijska karakteristika željenog oblika.

Na kraju, ukratko, navedimo korake u postupku projektovanja IIR filtra:

Analogne funkcije prenosa

Niskopropusni prototipi

Idealan niskopropusni filtar granične učestanosti 1 rad/s nije moguće napraviti. Zbog toga je funkciju prenosa analognog filtra potrebno aproksimirati racionalnom funkcijom koja će ličiti na idealni NF filtar. Takvih racionalnih funkcija ima mnogo, a mi ćemo navesti najznačajnije.

Prva aproksimacija idealne amplitudske karakteristike je svakako Batervortova (Butterworth) aproskimacija. Ona zadovoljava sledeći uslov:

$$ |H_B(j\omega)|^2 = \frac{1}{1 + \epsilon^2 \left( \omega/\omega_p \right) ^ {2N}}, $$

gde je $\omega_p$ granična učestanost propusnog opsega (najčešće ćemo uzimati da je $\omega_p = 1\, \mathrm{rad/s}$), $N$ je red filtra (red polinoma u brojiocu racionalne funkcije prenosa), a $\epsilon$ je parametar koji određuje slabljenje na granici propusnog opsega:

$$ \alpha_p = 20\log\left(\frac{1}{|H(j\omega_p)|}\right) = 10\log\left(\frac{1}{|H(j\omega_p)|^2}\right) = 10\log\left(1 + \epsilon^2 \right). $$

Ako se želi postići odgovarajuće slabljenje $\alpha_p$, tada se parametar $\epsilon$ mora postaviti na vrednost određenu prethodnim izrazom:

$$ \epsilon = \sqrt{10^{0,1\alpha_p}-1}. $$

Red filtra će odrediti slabljenje na graničnoj učestanosti nepropusnog opsega. Zbog toga se on određuje iz specifikacija zadatih za nepropusni opseg. Ako je zadata granična učestanost $\omega_a$ i minimalno slabljenje u nepropusnom opsegu $\alpha_a$, da bi funkcija prenosa zadovoljila tražene specifikacije, mora da važi:

$$ \alpha_a = 20\log\left(\frac{1}{|H(j\omega_a)|}\right) = 10\log\left(\frac{1}{|H(j\omega_a)|^2}\right) = 10\log\left(1 + \epsilon^2 \left( \omega_a/\omega_p \right) ^ {2N} \right). $$

Iz ovog izraza i izraza za parametar $\epsilon$ se dobija izraz za minimalni red filtra koji će zadovoljiti navedene specifikacije:

$$ N \geq \frac{\log \frac{10^{0,1\alpha_a} - 1}{10^{0,1\alpha_p} - 1}}{2 \log \left( \omega_a/\omega_p \right)}. $$

Vrednost desne strane navedenog izraza najčešće nije ceo broj pa se zbog toga za red filtra mora uzeti prvi sledeći veći ceo broj.

Ovde stajemo u opisu Batervortove aproksimacije, više detalja pogledajte u knjizi, prilično je neophodno za ispit. :) U našim programima ćemo koeficijente polinoma u brojiocu i imeniocu dobiti korišćenjem ugraćene funkcije iz Scipy biblioteke.

Druga aproksimacija koju moramo pomenuti je Čebiševljeva aproksimacija prve vrste kod koje važi:

$$ |H_C(j\omega)|^2 = \frac{1}{1 + \epsilon^2 T_N\left( \omega/\omega_p \right)}, $$

gde je $T_N(x)$ Čebiševljev polinom definisan rekurentnom formulom:

$$ T_{N+1}(x) = 2xT_N(x) - T_{N-1}(x), \; \;, T_0(x) = 1, \; \; T_1(x) = x. $$

Potreban red funkcije prenosa se dobija korišćenjem sledećeg izraza:

$$ N \geq \frac{\cosh ^{-1} \sqrt{D}}{\cosh ^{-1} ( 1/k )}, \; \; D = \frac{10^{0,1\alpha_a} - 1}{10^{0,1\alpha_p} - 1}, \; \; k = \omega_p/\omega_a. $$

Treća aproksimacija koju moramo pomenuti je Čebiševljeva aproksimacija druge vrste ili inverzna Čebiševljeva aproksimacija. Ona se dobija iz Čebiševljeve aproskimacije prve vrste tako što se u sledećem izrazu

$$ 1 - |H_C(j\omega)|^2 = \frac{\epsilon^2 T_N\left( \omega/\omega_p \right)}{1 + \epsilon^2 T_N\left( \omega/\omega_p \right)}, $$

argument Čebiševljevog polinoma zameni svojom recipročnom vrednošću

$$ |H_{IC}(j\omega)|^2 = \frac{\epsilon^2 T_N\left( \omega_p/\omega \right)}{1 + \epsilon^2 T_N\left( \omega_p/\omega \right)} $$

Potreban red funkcije prenosa se dobija korišćenjem istog izraza kao kod aproksimacije prve vrste.

Sledeća aproksimacija koju ćemo koristiti je Eliptička aproksimacija za koju važi:

$$ |H_E(j\omega)|^2 = \frac{1}{1 + C_N\left( \omega/\omega_p \right)}, $$

gde je $C_N(x)$ tzv. Čebiševljeva racionalna funkcija koja obezbeđuje oscilatorno ponašanje amplitudske karakteristike u propusnom i nepropusnom opsegu, kao i monotoni karakter u prelaznoj zoni. Na osnovu zadatkih specifikacija, potreban red filtra se određuje korišćenjem sledećih izraza:

$$ D = \frac{10^{0,1\alpha_a} - 1}{10^{0,1\alpha_p} - 1}, \; \; k = \sqrt{1 - \left(\frac{\omega_p}{\omega_a} \right)^2}, \; \; q_0 = \frac{1}{2} \frac{1-\sqrt{k}}{1+\sqrt{k}}, \; \; q = q_0 + 2q_0^5 + 15q_0^9 + 15q_0^{13}, \\ N \geq \frac{\log (16D)}{\log( 1/q )}. $$

Na kraju, treba pomenuti i Beselovu aproksimaciju čija je funkcija prenosa:

$$ H_{Bess}(j\omega) = \frac{1}{B_N(s)}, $$

gde je $B_N(x)$ Beselov polinom N-tog reda definisan rekurentnom formulom:

$$ B_{N}(x) = (2N-1)B_{N-1}(x) + x^2B_{N-2}(x), \; \;, B_0(x) = 1, \; \; B_1(x) = x+1. $$

Važna osobina ove aproksimacije je njena linearnost fazne karakteristike u propusnom opsegu. Međutim, ova osobina je od značaja ako se Beselova aproksimacija koristi prilikom projektovanja analognog filtra. Diskretizacijom će se linearnost faze poremetiti, tako da se za digitalne filtre koji imaju linearnu faznu karakteristiku uvek moraju odabrati filtri sa konačnim impulsnim odzivom. IIR filtri mogu samo imati manje ili više nelinearnu faznu karakteristiku.

Napišimo Pajton program koji će nacrtati frekvencijske karakteristike ovih prototipskih filtara. Pajton funkcije koje vraćaju analogne funkcije prenosa za navedene aproksimacije su:

z, p, k = signal.buttap(N)          # Vraća nule, polove i pojačanje Batervortovog filtra N-tog reda
z, p, k = signal.cheb1ap(N, Ap)     # Vraća nule, polove i pojačanje Čebiševljevog I filtra N-tog reda za definisano slabljenje na granici propusnog opsega
z, p, k = signal.cheb2ap(N, Aa)     # Vraća nule, polove i pojačanje Čebiševljevog II filtra N-tog reda za definisano slabljenje na granici nepropusnog opsega
z, p, k = signal.ellipap(N, Ap, Aa) # Vraća nule, polove i pojačanje eliptičkog filtra N-tog reda za definisana slabljenja na granicama propusnog i nepropusnog opsega
z, p, k = signal.besselap(N)        # Vraća nule, polove i pojačanje Beselovog filtra N-tog reda

Podrazumevana vrednost parametra $\epsilon$ je 1. Treba naglasiti da sve funkcije vraćaju filtre čija je granična učestanost propusnog opsega na $\omega_p = 1\, \mathrm{rad/s}$, osim inverzne Čebiševljeve (cheb2ap) koja vraća filtar čija je granična učestanost nepropusnog opsega na $\omega_a = 1\, \mathrm{rad/s}$. Koeficijente u brojiocu i imeniocu dobijamo iz korenova odgovarajućih polinoma korišćenjem funkcije np.poly().

Za određivanje frekvencijske karakteristike analogne funkcije prenosa, koristimo funkciju signal.freqs() (link). Za crtanje frekvencijske karakteristike možemo koristiti plot(), ali se često koristi i funkcija semilogx() kako bi se frekvencijska osa prikazala u logaritamskoj podeli.

Možemo uporediti i fazne karakteristike ovih filtara.

Dodatno, zanimljivo je projektovati filtar na osnovu zadatih specifikacija. Kao što smo ranije rekli, najpre je potrebno pronaći red filtra. U slučaju da se koristi Batervortova aproksimacija, potrebno je odrediti i parametar $\epsilon$ jer funkcija signal.buttap(N) vraća filtar čija je granična učestanost propusnog opsega podrazumevano $\omega_p = 1\, \mathrm{rad/s}$ i čije je dozvoljeno slabljenje u propusnom opsegu 3 dB. Ako traženo slabljenje u propusnom opsegu treba da bude drugačije od 3 dB, mora se preračunati novo $\epsilon$ i na odgovarajući način uvrstiti u vrednosti polova funkcije prenosa.

S obzirom na to da funkcija signal.buttap(N) vraća polove na jediničnom krugu, oni se moraju skalirati odgovarajućim parametrom u slučaju da je $\epsilon \neq 1$. Napišimo izraz za kvadrat amplitudske karakteristike u drugačijoj formi:

$$ |H_B(j\omega)|^2 = \frac{1}{1 + \epsilon^2 \left( \omega/\omega_p \right) ^ {2N}} = \frac{1}{1 + \left( \sqrt[N]{\epsilon} \frac{\omega}{\omega_p} \right) ^ {2N}} = \frac{1}{1 + \left( \frac{\omega}{\omega_p / \sqrt[N]{\epsilon} } \right) ^ {2N}}. $$

Iz ove jednakosti vidimo da polove čije je $\omega_p = 1\, \mathrm{rad/s}$ treba podeliti faktorom $\sqrt[N]{\epsilon}$. Međutim, ako to uradimo, promenićemo pojačanje funkcije prenosa u propusnom opsegu. Opšti oblik funkcije prenosa možemo zapisati kao racionalnu funkciju kompleksne promenljive $s$:

$$ H_B(s) = k \frac{\prod_{i = 1}^{M}(s - z_{i})}{\prod_{i = 1}^{N}(s - p_{i})}. $$

Znamo da na učestanosti $\omega = 0\, \mathrm{rad/s}$ funkcija prenosa ima vrednost 1, tj: $$ H_B(s=j0) = k \frac{\prod_{i = 1}^{M}(- z_{i})}{\prod_{i = 1}^{N}(- p_{i})} = 1. $$

Pogledajmo koliku vrednost ima na toj učestanosti ako podelimo polove faktorom skaliranja:

$$ H_{B2}(s=j0) = k \frac{\prod_{i = 1}^{M}(- z_{i})}{\prod_{i = 1}^{N}(- p_{i}/\sqrt[N]{\epsilon})} = k \frac{\prod_{i = 1}^{M}(- z_{i})}{\frac{1}{\epsilon}\prod_{i = 1}^{N}(- p_{i})} = \epsilon k \frac{\prod_{i = 1}^{M}(- z_{i})}{\prod_{i = 1}^{N}(- p_{i})} = \epsilon H_B(s=j0) = \epsilon. $$

Dakle, deljenjem polova utičemo i na vrednost amplitudske karakteristike. Da bi ona ponovo bila jednaka 1, pojačanje $k$ se mora podeliti sa $\epsilon$.

Napomena: Skaliranje polova ne treba raditi ako se koriste druge aproksimacije jer funkcije vraćaju već skalirane vrednosti pošto im se prosleđuju parametri slabljenja.

Transformacije učestanosti

Kada je poznata funkcija prenosa NF filtra, odgovarajućim smenama kompleksne promenljive $s$ se mogu dobiti NF filtar drugih graničnih učestanosti, VF filtar, PO filtar i NO filtar. Ovaj postupak se naziva transformacijom učestanosti.

NF u NF

Transformacija iz NF prototipa čije su granične učestanosti $\omega_p$ i $\omega_a$ u drugi NF filtar graničnih učestanosti $\hat{\omega}_p$ i $\hat{\omega}_a$ se dobija smenom: $$ H_{NF}(\hat{s}) = H_{NF}(s)|_{s=a\hat{s}}, $$

gde je $$ a = \frac{\omega_p}{\hat{\omega}_p} = \frac{\omega_a}{\hat{\omega}_a}. $$

U Pajtonu možemo normalizovanu prototipsku funkciju lako transformisati korišćenjem funkcije lp2lp. Potrebno je samo proslediti koeficijente normalizovanog prototipa i željenu graničnu učestanost propusnog opsega:

b, a = signal.lp2lp(bn, an, wp)

S obzirom na to da funkcija cheb2ap daje normalizovani prototim kome je granična učestanost nepropusnog opsega $1 \mathrm{rad/s}$ onda se mora o tome voditi računa. Ako je normalizovani prototip dobijen inverznom Čebiševljevom aproksimacijom, onda se njegova transformacija učestanosti radi korišćenjem iste funkcije, samo što se umesto wp, granične učestanosti propusnog opsega filtra koji se projektuje, stavi wa, granična učestanost nepropusnog opsega filtra koji se projektuje.

NF u VF

Transformacija iz NF prototipa čije su granične učestanosti $\omega_p$ i $\omega_a$ u VF filtar graničnih učestanosti $\hat{\omega}_p$ i $\hat{\omega}_a$ se dobija smenom: $$ H_{VF}(\hat{s}) = H_{NF}(s)|_{s=a/\hat{s}}, $$

gde je $$ a = \omega_p \hat{\omega}_p = \omega_a \hat{\omega}_a. $$

U Pajtonu možemo normalizovanu prototipsku funkciju lako transformisati korišćenjem funkcije lp2hp. Potrebno je samo proslediti koeficijente normalizovanog prototipa i željenu graničnu učestanost propusnog opsega:

b, a = signal.lp2hp(bn, an, wp)

Ako je normalizovani prototip dobijen inverznom Čebiševljevom aproksimacijom, onda se njegova transformacija učestanosti radi korišćenjem iste funkcije, samo što se umesto wp, granične učestanosti propusnog opsega filtra koji se projektuje, stavi wa, granična učestanost nepropusnog opsega filtra koji se projektuje.

NF u PO

Transformacija iz NF prototipa čije su granične učestanosti $\omega_p$ i $\omega_a$ u PO filtar se dobija smenom: $$ H_{PO}(\hat{s}) = H_{NF}(s)|_{s=\frac{\hat{s}^2 + \omega_0^2}{B\hat{s}}}, $$

gde je $\omega_0$ centralna učestanost propusnog opsega, a $B$ skalirana širina propusnog opsega za koje važe sledeće jednakosti:

$$ \omega_0^2 = \hat{\omega}_{p1} \hat{\omega}_{p2} = \hat{\omega}_{a1} \hat{\omega}_{a2}, \; \; B = (\hat{\omega}_{p2} - \hat{\omega}_{p1})/\omega_{p}. $$

U Pajtonu možemo normalizovanu prototipsku funkciju lako transformisati korišćenjem funkcije lp2bp. Potrebno je samo proslediti koeficijente normalizovanog prototipa, željenu centralnu učestanost propusnog opsega i skaliranu širinu propusnog opsega:

b, a = signal.lp2bp(bn, an, w0, B)

Ako je normalizovani prototip dobijen inverznom Čebiševljevom aproksimacijom, onda se njegova transformacija učestanosti radi korišćenjem iste funkcije, centralna učestanost se isto definiše, ali se skalirani propusni opseg $B$ drugačije definiše i to kao $B = (\hat{\omega}_{a2} - \hat{\omega}_{a1})/\omega_a$, jer slabljenje koje se prosleđuje funkciji za generisanje koeficijenata normalizovanog filtra inverzne Čebiševljeve aproksimacije odgovara učestanosti $\hat{\omega}_{a}$.

NF u NO

Transformacija iz NF prototipa čije su granične učestanosti $\omega_p$ i $\omega_a$ u NO filtar se dobija smenom: $$ H_{NO}(\hat{s}) = H_{NF}(s)|_{s=\frac{B\hat{s}}{\hat{s}^2 + \omega_0^2}}, $$

gde je $\omega_0$ centralna učestanost nepropusnog opsega, a $B$ skalirana širina nepropusnog opsega za koje važe sledeće jednakosti:

$$ \omega_0^2 = \hat{\omega}_{p1} \hat{\omega}_{p2} = \hat{\omega}_{a1} \hat{\omega}_{a2}, \; \; B = (\hat{\omega}_{p2} - \hat{\omega}_{p1})\omega_{p}. $$

U Pajtonu možemo normalizovanu prototipsku funkciju lako transformisati korišćenjem funkcije lp2bs. Potrebno je samo proslediti koeficijente normalizovanog prototipa, željenu centralnu učestanost nepropusnog opsega i skaliranu širinu nepropusnog opsega:

b, a = signal.lp2bs(bn, an, w0, B)

Ako je normalizovani prototip dobijen inverznom Čebiševljevom aproksimacijom, onda se njegova transformacija učestanosti radi korišćenjem iste funkcije, centralna učestanost se isto definiše, ali se nepropusni opseg $B$ drugačije definiše i to kao $B = (\hat{\omega}_{a2} - \hat{\omega}_{a1})\omega_a$, jer slabljenje koje se prosleđuje funkciji za generisanje koeficijenata normalizovanog filtra inverzne Čebiševljeve aproksimacije odgovara učestanosti $\hat{\omega}_{a}$.

Parametri normalizovanog prototipa

Kao što smo više puta ponovili, prvi korak u projektovanju filtra je sinteza odgovarajućeg normalizovanog NF prototipa. Međutim, specifikacije filtra koje su nam na raspolaganju odgovaraju finalnom filtru koji treba da dobijemo iz normalizovanog NF prototipa transformacijom učestanosti. Iz smena za komleksnu promenljivu $s$ se mogu naći veze između specifikacija filtra koji se projektuje i specifikacija normalizovanog NF prototipa.

Najpre, slabljenja u propusnom i nepropusnom opsegu normalizovanog NF prototipa su ista kao kod filtra koji je potrebno projektovati. Ovim metodom nije moguće projektovati funkcije prenosa koje u različitim propusnim ili različitim nepropusnim opsezima imaju različito slabljenje. Da bi se ovo postiglo, morala bi se projektovati kaskadna veza više filtara različitih specifikacija.

Ostaje da vidimo koje su vrednosti za specifikacije graničnih učestanosti normalizovanog NF prototipa. Jasno, čim je normalizovan, granična učestanost propusnog opsega je $\omega_p = 1\, \mathrm{rad/s}$. Granična učestanost nepropusnog opsega se izvodi iz izraza za smenu kompleksne promenljive. Ovde navodimo veze koje se izvode:

NF u NF:

$$ \omega_a = \frac{\hat{\omega}_a}{a} = \frac{\hat{\omega}_a}{\hat{\omega}_p/\omega_p} = \frac{\hat{\omega}_a}{\hat{\omega}_p}\, \mathrm{rad/s} $$

NF u VF:

$$ \omega_a = \frac{a}{\hat{\omega}_a} = \frac{\hat{\omega}_p \omega_p}{\hat{\omega}_a} = \frac{\hat{\omega}_p}{\hat{\omega}_a}\, \mathrm{rad/s} $$

NF u PO:

$$ \omega_a = -\frac{\omega_0^2 - \hat{\omega}_{a2}^2}{B\hat{\omega}_{a2}} = \omega_{p} \frac{\hat{\omega}_{a2}^2 - \omega_0^2}{(\hat{\omega}_{p2} - \hat{\omega}_{p1})\hat{\omega}_{a2}} = \frac{\hat{\omega}_{a2}^2 - \omega_0^2}{(\hat{\omega}_{p2} - \hat{\omega}_{p1})\hat{\omega}_{a2}}\, \mathrm{rad/s} $$

NF u NO:

$$ \omega_a = \frac{B\hat{\omega}_{a1}}{\omega_0^2 - \hat{\omega}_{a1}^2} = \omega_{p} \frac{(\hat{\omega}_{p2} - \hat{\omega}_{p1})\hat{\omega}_{a1}}{\omega_0^2 - \hat{\omega}_{a1}^2} = \frac{(\hat{\omega}_{p2} - \hat{\omega}_{p1})\hat{\omega}_{a1}}{\omega_0^2 - \hat{\omega}_{a1}^2}\, \mathrm{rad/s} $$

Primenimo sada transformacije učestanosti kako bismo dobili odgovarajuće filtre. Korišćenjem normalizovanog Batervortovog prototipa ćemo projektovati sledeće filtre:

Diskretizacija

Diskretizacijom analogne funkcije prenosa dobijamo funkciju prenosa digitalnog filtra. Postoji više načina da se ovo uradi. U ovom uvodu ćemo navesti dva, a u programima ćemo koristiti najčešće jedan od ta dva načina.

Da bi se diskretizacija uradila ispravno, potrebno je da transformacija iz analogne u digitalnu funkciju prenosa zadovoljava sledeće osobine:

Impulsno invarijantna transformacija

Prirodan način za diskretizaciju sistema je najprostija diskretizacija njegovog impulsnog odziva. Na ovaj način se dobija takozvana impulsno invarijantna transformacija. Cilj ove transformacije je da i u diskretnom domenu, impulsni odziv funkcije prenosa u potpunosti zadrži isti oblik kao u analognom domenu. S obzirom na to da impulsni odziv zadržava isti oblik, amplitudska karakteristika takođe neće promeniti oblik, ali pod uslovom da je pri diskretizaciji zadovoljena teorema odabiranja. Dakle, ako je učestanost odabiranja $f_s$ značajno veća od maksimalne učestanosti u spektru analognog filtra, impulsno invarijantna trasnformacija će raditi lepo, sve analogne učestanosti $\omega$ će se preslikati u digitalne učestanosti $\Omega = \omega T_s$ i amplitudska karakteristika neće biti izobličena. Međutim, ovo ograničenje je izuzetno strogo. To znači da impulsno invarijantnom transformacijom možemo projektovati samo filtre kojima je amplitudska karakteristika na velikim učestanoma izuzetno mala, praktično jednaka nuli. Takvi filtri su samo filtar propusnik niskih učestanosti i filtar propusnik opsega učestanosti. Filtar propusnik visokih učestanosti i filtar nepropusnik opsega učestanostia se ne mogu napraviti korišćenjem impulsno invarijantne transformacije. Zbog toga ona i ne postoji u paketu scipy.signal.

U primerima za ove vežbe ćemo koristiti drugu transformaciju, a impulsno invarijantna transformacija ostaje kao važan teorijski pojam i, naravno, srešćete je na ispitu.

Bilinearna transformacija

Kako bi se izvela transformacija koja omogućava diskretizaciju svih tipova filtara treba setiti jedne važne osobine analognih filtara: Svaka analogna funkcija prenosa se može predstaviti pomoću dijagrama toka u kome eksplicitno figurišu grane sa integratorima koje jedino zavise od učestanosti karakterističnih za tu funkciju prenosa. Dakle, ideja je u diskretizaciji integratora, tj. u nekoj vrsti diskretne aproksimacije integrala.

Neka je $y(t)$ neki analogni signal koji predstavlja integral po vremenu analognog signala $x(t)$

$$ y(t) = \int_{0}^{t} x(\tau)d\tau. $$

To znači da je prenosna funkcija integratora

$$ H(s) = \frac{Y(s)}{X(s)} = \frac{1}{s}. $$

Razliku između vrednosti signala $y(t)$ u dva različita trenutka možemo odrediti određenim integralom signala $x(t)$

$$ y(t_2) - y(t_1) = \int_{0}^{t_2} x(\tau)d\tau - \int_{0}^{t_1} x(\tau)d\tau = \int_{t_1}^{t_2} x(\tau)d\tau. $$

Ako diskretizujemo signale $x(t)$ i $y(t)$ sa periodom odabiranja $T_s$, onda prethodni izraz važi i za susedne odbirke signala $y$:

$$ y(kT_s) - y(kT_s-T_s) = \int_{kT_s-T_s}^{kT_s} x(\tau)d\tau. $$

Dakle, razlika dva susedna odbirka predstavlja površinu ispod funkcije $x(t)$. Ova površina se može aproskimirati površinom trapeza čija su temena u tačkama $(kT_s-T_s, x(kT_s-T_s))$, $(kT_s, x(kT_s))$, $(kT_s-T_s, 0)$ i $(kT_s, 0)$

$$ y(kT_s) - y(kT_s-T_s) \approx T_s \frac{x(kT_s - T_s) + x(kT_s)}{2}. $$

Primenom Z transformacije na obe strane jednakosti dobijamo: $$ \mathcal{Z} \left\lbrace y[k] - y[k-1] \right\rbrace = \mathcal{Z} \left\lbrace T_s \frac{x[k-1] + x[k]}{2} \right\rbrace \\ \Downarrow \\ Y(z)(1 - z^{-1}) = \frac{T_s}{2} X(z) (1 + z^{-1}) \\ \Downarrow \\ \frac{Y(z)}{X(z)} = \frac{T_s}{2} \frac{1 + z^{-1}}{1 - z^{-1}}. $$

Dakle, prenosna funkcija diskretnog integratora je određena gornjim izrazom. Imajući u vidu da je prenosna funkcija analognog integratora $1/s$, diskretizacija funkcije prenosa se može postići smenom kompleksne promenljive $s$ i odgovarajućeg izraza po $z$, a koji je na osnovu prethodne analize:

$$ \frac{1}{s} = \frac{T_s}{2} \frac{1 + z^{-1}}{1 - z^{-1}} \\ \Downarrow \\ s = \frac{2}{T_s} \frac{1 - z^{-1}}{1 + z^{-1}} $$

Ova transformacija se naziva bilinearnom transformacijom.

Bilinearnu trasnformaciju u Pajtonu možemo primeniti preračunavanjem koeficijenata, ali postoji ugrađena funkcija iz paketa scipy.signal koja to radi umesto nas. Kao argumente prima koeficijente analogne funckije prenosa i učestanost odabiranja, a vraća koeficijente diskretizovane funckije prenosa:

[bd, ad] = signal.bilinear(b, a, fs)

Primenimo ovu transformaciju na analogne funkcije prenosa filtara projektovanih u prethodnim primerima. Dodatno, nacrtajmo amplitudske karakteristike digitalnog i analognog filtra jednu preko druge.

Napomena: U narednom primeru su i specifikacije filtra malo relaksirane jer se koristi Batervortov prototip koji zahteva dosta veliki red za specifikacije iz prethodnog primera.

Možemo primetiti da amplitudska karakteristika digitalnog filtra odstupa u određenoj meri od amplitudske karakteristike analognog filtra. Razlog za ovu osobinu bilinearne transformacije je nelinearno preslikavanje učestanosti iz analognog u digitalni domen. Ovo preslikavanje se vrlo jednostavno može izvesti iz smene, ako se umesto kompleksnih promenljivih $s$ i $z$ stave njihovi ekvivalenti u Furijeovim transformacija.

$$ s = \frac{2}{T_s} \frac{1 - z^{-1}}{1 + z^{-1}} \\ \Downarrow \\ j\omega = \frac{2}{T_s} \frac{1 - e^{-j\Omega}}{1 + e^{-j\Omega}} = \frac{2}{T_s} \frac{e^{-j\Omega/2}}{e^{-j\Omega/2}} \frac{e^{j\Omega/2} - e^{-j\Omega/2}}{e^{j\Omega/2} + e^{-j\Omega/2}} \\ \Downarrow \\ \omega = \frac{2}{T_s} \frac{e^{j\Omega/2} - e^{-j\Omega/2}}{2j} \frac{2}{e^{j\Omega/2} + e^{-j\Omega/2}} = \frac{2}{T_s} \frac{\sin{\frac{\Omega}{2}}}{\cos{\frac{\Omega}{2}}} = \frac{2}{T_s} \tan{\frac{\Omega}{2}} \Downarrow \\ \omega = \frac{2}{T_s} \tan{\frac{\Omega}{2}} $$

Dodatno, ako se uveličaju pojedini delovi amplitudske karakteristike, može se pimetiti da digitalna funkcija prenosa ne zadovoljava specifikacije. Ovo se upravo dešava zbog nelinearnog preslikavanja učestanosti i naziva se distorzija. Zbog toga je prilikom projektovanja filtra definisanih specifikacija neophodno uraditi predistorziju, tj. podešavanje specifikacija analogne funkcije prenosa tako da, nakon bilinearne transformacije i distorzije učestanosti, dobijeni filtar zadovolji specifikacije.

Projektovanje IIR filtara na osnovu zadatih specifikacija

Konačno, evo primera projektovanja digitalnog filtra na osnovu zadatih specifikacija. Koristićemo bilinearnu transformaciju. Moramo voditi računa o tome da ispravno podesimo specifikacije analognog prototipa. Sve ovo ćemo uraditi na primeru.

PRIMER: Na slici je prikazan sistem za digitalnu obradu signala. Učestanost odabiranja u sistemu je $f_s = 50\, \mathrm{kHz}$.

Sistem prikazan na slici se ponaša kao propusnik opsega učestanosti sa sledećim karakteristikama:

Odrediti funkciju prenosa (koeficijente polinoma u brojiocu i imeniocu funkcije prenosa) digitalnog IIR filtra $H(z)$ tako da sistem zadovolji zadate specifikacije. Red funkcije prenosa treba da bude minimalan. Prikazati dobijeni red funcije prenosa.

Generisati frekvencijski odziv funkcije prenosa u 10000 tačaka i nacrtati amplitudsku karakteristiku frekvencijskog odziva posmatranog sistema u dB u opsegu učestanosti od $0$ do $f_s/2$. Frekvencijska osa treba da bude u linearnoj razmeri. Smatrati da su analogni filtri u sistemu idealni. Na grafiku amplitudske karakteristike, crvenim linijama nacrtati gabarite projektovanog filtra.

Na ulaz sistema dolazi signal $x(t) = \cos(2\pi f_{p1}t) + \cos(2\pi f_{p2}t) + \cos(2\pi f_{a1}t) + \cos(2\pi f_{a2}t)$. Generisati signal $x[n]$ u 1024 tačke i nacrtati amplitudsku karakteristiku njegovog spektra. Generisati signal y[n] i nacrtati amplitudsku karakteristiku njegovog spektra. Amplitudske karakteristike crtati u prirodnom opsegu učestanosti od $0$ do $f_s/2$.

Iz specifikacija lako zaključujemo da su granične učestanosti propusnog opsega $f_{p1} = f_{a1} + B_t = 9\, \mathrm{kHz}$ i $f_{p2} = f_{a2} - B_t = 10\, \mathrm{kHz}$. Dakle digitalni filtar ima sledeće granične učestanosti $\Omega_{p1} = 2\pi f_{p1}/f_s$, $\Omega_{p2} = 2\pi f_{p2}/f_s$, $\Omega_{a1} = 2\pi f_{a1}/f_s$ i $\Omega_{a2} = 2\pi f_{a2}/f_s$. Da bi digitalni filtar imao ove granične učestanosti nakon bilinearne transformacije, analogni prototip moramo projektovati tako da mu granične učestanosti odgovaraju učestanostima

$$ \omega_{ai/pi} = \frac{2}{T_s} \tan{\frac{\Omega_{ai/pi}}{2}}, $$

gde je indeksom $ai/pi$ obeležena bilo koja granična učestanost. Specifikacije slabljenja, naravno, ostaju iste. Kada smo dobili specifikacije analognog prototipa, dalji postupak se svodi na njegovo projektovanje koje smo već naučili na prethodnim primerima. Najpre je potrebno naći granične učestanosti normalizovanog NF prototipa, zatim projektovati normalizovani NF prototip. Kad njega imamo, vraćamo se unazad: transformacija učestanosti i bilinearna transformacija.

Prilikom proračuna specifikacija analognog prototipa moramo voditi računa o tome da se granična učestanost nepropusnog opsega računa na osnovu izraza

$$ \omega_a = \frac{\hat{\omega}_{a2}^2 - \omega_0^2}{B\hat{\omega}_{a2}} $$

i da je $B = (\hat{\omega}_{p2} - \hat{\omega}_{p1})/\omega_{p1} = (\hat{\omega}_{p2} - \hat{\omega}_{p1})/1\, \mathrm{rad/s}$ i $\omega_0^2 = \hat{\omega}_{p2} \hat{\omega}_{p1}$. To jest, moramo voditi računa o tome da u izrazu za $\omega_a $ normalizovanog prototipa nigde ne figuriše granična učestanost prvog nepropusnog opsega. To je u redu, ali moramo znati da će nakon transformacije učestanosti ona biti

$$ \hat{\omega}_{a1} = \frac{\omega_0^2}{\hat{\omega}_{a2}}, $$

to jest: na nju ne možemo da utičemo. Međutim, ako su specifikacije filtra takve da je ova učestanost manja od specificirane, gabariti filtra neće biti zadovoljeni. Zbog toga, moramo pooštriti specifikacije drugih graničnih učestanosti da bi se zadovoljio gabarit za $\omega_{a1}$. Najlakše je to uraditi tako što se pooštri gabarit za graničnu učestanost drugog nepropusnog opsega i to tako da nakon transformacije učestanosti sigurno bude zadovoljena i granična učestanost prvog nepropusnog opsega. Da biste videli ovaj efekat, možete podesiti da su sepcifikacije drugačije, na primer da je $f_{p1} =8,25\, \mathrm{kHz}$.

Projektovanje IIR filtara korišćenjem ugrađenih funkcija Scipy biblioteke

Na kraju, veoma je važno da pomenemo da biblioteka scipy.signal ima funkcije za projektovanje digitalnih filtara na osnovu specifikacija koje im zadamo. Najkorisnija je funkcija signal.iirdesign(...) kojoj je dovoljno proslediti specifikacije, tip željenog prototipa i nekoliko dodatnih opcija. Ona će na osnovu tih podataka uraditi sve ovo što smo mi do sada radili korak po korak i vratiće koeficijente filtra. Postoji još funkcija, ceo paket i sve funkcije možete pronaći ovde.

S obzirom na to da je ovo osnovni kurs, morali smo da prođemo kroz metode projektovanja filtara. U budućnosti se može desiti da zatreba, ali je mnogo veća verovatnoća da ćete filtre dizajnirati korišćenjem ugrađenih funkcija.